Standard Error of Measurement (SEM)
Standard Error of Measurement (SEM)
The SEM enables us to estimate the amount by which a student’s obtained score might differ from the student’s true score. Chapter 10, “Establishing Evidence of Reliability and Validity,” discuss the implications of the SEM on test score interpretation.
The SEM is very important because, if we assume that an obtained score on a test is necessarily the student’s true score, we will misinterpret the test results (Reynolds et al., 2008). The SEM for our sample in Table 11.1 is 3.8, which means that the true score for an observed raw score of 72 would range between 68.2 and 75.8. This range is referred to as the confidence band.
Suppose that the passing score on a test was predetermined to be 75. Would you consider adding 4 points to all scores on the test if the SEM was a 4? While it is not advisable to add points, or scale grades, for each individual test, if you are inclined to scale the grades, it is a better practice to wait for the final grade. Suppose you scale up the grades three points for exam one and the scores on exam two are very high. Will you scale down the scores for exam two? You probably would cause a student revolt.
GET ASSIGNMENT HELP HERE
Scaling individual test scores can alter the predetermined weighting of the components of the course grade. The better practice is to wait until the end of the course; look carefully at the means, medians, reliability coefficients, and SEMs for all exams; consider the final score spread; and then add points (if you judge it necessary) to the final grade assignment (refer to the discussion on grading in Chapter 13, “Assigning Grades”).
The important lesson to be learned from the Standard Error of Measurement (SEM) is that classroom test scores are not absolute, and they do not represent students’ true scores. Measurement error is present in all scores, so you must look at the margin of error in a test and be flexible when translating raw scores into test scores and test scores into course grades. If the statistical analysis provided by your test development software does not provide the SEM, you can calculate it by using the formula in Exhibit 10.5.
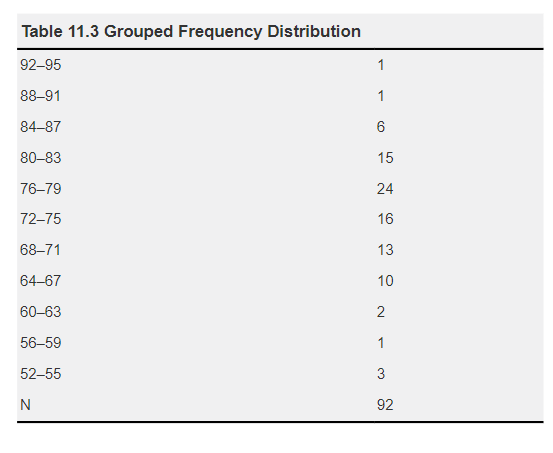
Score DistributionA test score distribution complements the analysis of test data by providing you with a description of how the class as a whole performed on the test. A distribution helps you visualize test results and makes the scores easier to interpret. Score distributions are typically reported in a frequency table or in a graphic format.Table 11.3 is a grouped frequency distribution associated with the sample data in Table 11.1. This frequency distribution groups the raw scores on the test into four-point intervals. In this distribution, you can see, for example, that six students scored from 84 to 87. This distribution provides a visual representation for interpreting the range of raw scores on a test. It enables you to visualize the significance of test analysis data such as the mean and the median and to identify how the scores on the test are clustered Standard Error of Measurement (SEM).